【速報】大学入学共通テスト2022 数学Ⅱ・Bの問題・解答・分析一覧

2022.01.16

データネット実行委員会（ベネッセコーポレーション・駿台予備学校共催）による2022年度大学入学共通テストの「数学Ⅱ・数学Ｂ」の問題分析は次の通り。

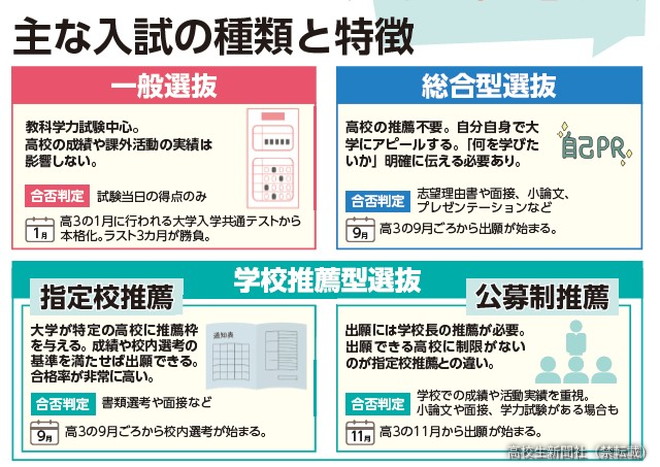
「図形と方程式」や現実事象を扱う問題（数列）が出題された。昨年よりやや難化

第１問〔１〕において、2019年度センター追試験以来みられなかった「図形と方程式」の出題があった。第４問「数列」では、現実事象を扱った対話文を含む問題が出題された。第５問「ベクトル」では、対話文をもとに考察を進めていく平面ベクトルの問題が出題された。全体を通して幅広い知識の活用が求められ、平均点が高かった昨年と比べてやや難化。

大問数・解答数

昨年と同様５大問で、第１問・第２問は必答、第３問～第５問から２大問を選択する形式。第１問・第２問は２中問構成であった。

出題形式

昨年と同様、数字を答える形式が中心で、選択肢から選ぶ問題は24～25問であった（解答数25～28）。

出題分野

例年同様、特定の分野に偏ることなく幅広く出題された。第１問〔１〕は「図形と方程式」からの出題であり、後半部分では「三角関数」の内容が扱われた。

問題量

総ページ数は19～21ページ（計算用紙を除く）で、昨年より５ページ増加した。

難易

昨年よりやや難化。

大問別分析

第1問「図形と方程式」、「三角関数」、「指数関数・対数関数」（30点・標準）　数学IIと共通　必答

〔１〕は、円と定点を通る直線が共有点をもつ条件を求める問題。直線の傾きを２次方程式が重解をもつ条件とtanの２倍角の公式を利用して、２通りの方法で考える設定。〔２〕は、底と真数を入れ替えた対数の大きさを考察する問題。（３）では、太郎さんの考察した内容をしっかり理解し、（４）では、（３）で得られた条件式に数値を代入して、対数の大小関係を正しく把握できればよい。

第2問「微分法・積分法」（30点・標準）　数学IIと共通　必答

〔１〕（１）は、３次関数のグラフの概形を選択する問題。（２）、（３）では、その増減・極値と３次方程式の実数解の個数について考察する問題であった。（３）の命題の真偽について考察する問題が目新しかった。〔２〕は、２つの３次関数のグラフなどからなる図形の面積の立式を、選択肢から選び、その面積を計算する問題。〔１〕、〔２〕ともに微分法・積分法の分野におけるオーソドックスな内容であった。

第3問「確率分布と統計的な推測」（20点・やや易）　選択

２つの地区で収穫されるジャガイモの個数や重さについて考察する問題。（１）、（２）は200gを超えるジャガイモの個数に関して平均値などを求める問題。二項分布の性質を正しく理解し、正規分布表を正しく用いて数値を読み取ることができれば、解答することができる。（３）はジャガイモ１個の重さを表す確率変数Ｘの確率密度関数の係数を決定する問題。基本的な内容で、計算も比較的取り組みやすいものであった。

第4問「数列」（20点・やや難）　選択

歩行者と自転車が移動と停止を繰り返したときのそれぞれの位置（座標）を数列の漸化式を用いて考察する問題。a2、b2は与えられたグラフを利用して求めればよい。（１）の後半は、花子さんと太郎さんの対話をヒントに条件を正しく理解できたかどうかで差がついたであろう。anとbnの漸化式が得られた後は、等比数列、階差数列の考え方を利用すればan、bnそれぞれの一般項を求めることができる。（２）では、（１）で求めた一般項をもとに、自転車が歩行者に追いつく回数や時刻を求める問題が出題された。

第5問「ベクトル」（20点・標準）　選択

単位円周上に３点Ａ、Ｂ、Ｃがあり、ベクトルOAとベクトルOBの内積の値が与えられている。まず、正確に図をかくことが必要があった。（１）は内分の公式や垂直の条件を用いて丁寧に計算すればよい。（２）はｔの値によって点Ｑが４つのどの部分に含まれるかを考察する問題。Ｐは内分点なので、ｔの値によってｋの正負がどのように変化するかに着目すればよい。（３）は対話文の誘導に従えば複雑な計算をしなくてよい。